Serendipity, Success, and Queueing Theory

An overly simple model of success might be:

1. Opportunities present themselves according to some distribution ¹, with the payout from an opportunity largely a function of the opportunity’s likelihood (the rarer, the higher the payout).
2. An individual can take on an opportunity if they are able to process it within a certain time ².
3. Success is the sum of all opportunities.
4. Due to the long-tailed nature of opportunities, an individual’s success is, to a significant degree, due to rare but impactful opportunities.

The above model might be called the serendipity model of success. If true, how should we think about taking on work?

The Individual as a Queue

If it wasn’t obvious, the above model has been setup to be amenable to being approached via queueing theory. An individual can be seen as a server which receives requests according to some distribution and takes time to process those requests according to a different distribution. An important intuition one can derive from queueing theory is a trade-off between utilization and waiting time (illustrated in the below graph). As the number of requests an individual takes on approaches their serving capacity, the expected waiting time for processing a given request explodes, increasing rapidly (note, M/M/1 models do not account for priority nor switching costs).

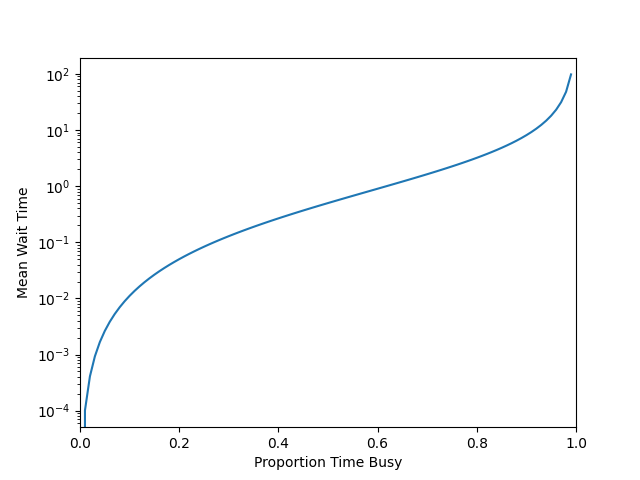Queue length vs proportion time busy for a M/M/1 queue

With this in mind, an individual who ensures that are too heavily utilized is ultimately harming their likelihood of long run success. If too busy, you don’t have time for serendipity.

Priority not a Priority

One objection to the above model is that it doesn’t take into account priority. This is true, but doesn’t change the conclusion (much). Realistic priority models often take into account switching costs and enable higher “individual level” utilization, but switching costs are seldom a real world constraint. Importantly, this is simply because, to paraphrase a potentially questionable project management adage: the work expands to fill the space.

Instead of switching costs, the binding constraint is often commitment costs. If you commit to working on a high priority project for two weeks, your ability to commit to other (higher priority) projects will be diminished over the next two weeks. This suggests a second important corollary of the serendipity model of success: the value of a project is a largely a function of it’s importance and the effort necessary to bring that project to fruition. The best projects are relatively cheaper than average while being relatively more expensive.

When Switching Costs Matter

In practice, you are not a M/M/1 queue. You might be a queue of some sort, but a better analogy might be an operating system scheduler. You are capable of commiting to some number of tasks at a time, and are able to allocate your finite computational capacity across these active tasks. Due to commitment costs, you can’t just switch to “the most important task”, preventing a certain type of thrashing. You, however, can find yourself prone to a separate type of thrashing.

As you commit yourself to more and more projects, the average computational capacity allocated to each project, by necessity, decreases. Beyond a certain threshold, switching costs begin to dominate and grow non-linearly with each additional task. This suggests that, in addition to project importance and effort, you should pay attention to the number of committed tasks. To maximize serendipity, you might want to focus on a small number of relatively low cost relatively high importance tasks ³.